يصنف المثلث الذي امامك وفقا للاضلاع بانه

السؤال :- يصنف المثلث الذي أمامك وفقا للاضلاع بأنه …..* حل سؤال من اختبارات الصف اول ثانوي يعتبر هذا السؤال أختار الإجابة الصحيحة: يصنف المثلث الذي أمامك وفقا للاضلاع بأنه ….. متطابق الضلعين متطابق الأضلاع مختلف الأضلاع متطابق الزوايا، من أسئلة الرياضيات حيث تحتوي المناهج السعودية على الكثير من أسئلة الرياضيات التي تحتاج إلى تفكير وتحليل للمسالة قبل حلها، وقبل أن ننتقل إلى عزيزي الطالب يجب أن تعلم حل السؤال يصنف المثلث الذي امامك وفقا للاضلاع بانه ، والآن سننتقل إلى حل السؤال المقال وهو يصنف المثلث الذي امامك وفقا لزواياه بانه ….مطلوب الإجابة. خيار واحد. (1 نقطة) من وقت أن بدأ العام الدراسي الجديد ويبدأ الطلاب والطالبات بالبحث عن الاجابات الصحيحة والنموذجية الخاصة بأسئلة الكتاب المدرسي الخاصة بهم، واليوم من خلال الموقع المثالي يسعدنا ان نقدم الاجابة عن اهم سؤال من ضمن اسئلة كتاب الطالب رياضيات اول ثانوي ف1 وهو السؤال يصنف المثلث الذي أمامك وفقا للاضلاع بأنه، والإجابة الصحيحة فيما ياتي.

ما هي نظرية فيتاغورس

ان نظرية فيثاغورس أحد أشهر النظريات التي عرفها علم الرياضيات، فقد تم وضع نظرية فيثاغورس على يد العالم اليوناني المعروفة باسمه تلك النظرية فيثاغورس، ولكن تلك النظرية الهامة يتم استخدامها بشكل خاص مع المثلث ذات الزاوية القائمة، تلك النظرية التي تنص على ان تلك المساحة الخاصة بالمربع المنشأ على الوتر، يساوي مساحة المربعين الذين يقعوا على الضلعي القائمين، ويمكن صياغة تلك النظرية على انها.

مربع طول الوتر يساوي مربع الضلع القائم الأول زائد مربع الضلع القائم الثاني.

مثال، اذا كان لدينا مثلث أ ب ج، وهو مثلث قائم الزاوية في النقطة ب، كما ان العلاقة بين اطوال الاضلاع هي، أج^2 يساوي أب^2 زائد أج^2.

يصنف المثلث الذي امامك وفقا للاضلاع بانه

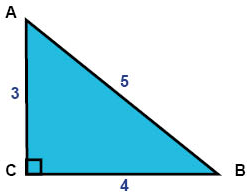
أختر الإجابة الصحيحة: السؤال :- يصنف المثلث الذي أمامك وفقا للاضلاع بأنه …..*

• متطابق الضلعين
• متطابق الأضلاع
• مختلف الأضلاع
• متطابق الزوايا

والإجابة الصحيحة والتي يتناولها سؤال يصنف المثلث الذي أمامك وفقا للاضلاع بأنه، كانت هي عبارة عن ما يلي:

في المثلث القائم الزاوية أعلاه زاوية الرأس C هي زاوية قائمة. وهذا يعني أن الضلعين اللذيّن طولهما 3 و 4 وحدة طولية هما ضلعي المثلث القائميّن. أما الضلع الثالث الذي طوله 5 هو وَتَر المثلث.

وفقا لنظرية فيثاغورس ستنطبق العلاقة التالية بين أضلاع المثلث:

52=42+32

لنتحقق مما إذا كان هاذين الطرفين متساويين أم لا، وذلك بتبسيط الطرفين الأيمن والأيسر كل على حدة.

الطرف الأيمن =

=42+32

=4⋅4+3⋅3=

=16+9=

25=

الطرف الأيسر =

=52

=5⋅5=

25=

الطرف الأيمن يساوي الطرف الأيسر. إذن نظرية فيثاغورس صالحة لهذا المثلث.

في حالة عدم تساوي الطرفين الأيمن والأيسر، فهذا يعني أن طول أحد أضلاع المثلث خطأ أو قد لا يكون المثلث قائم الزاوية. عليه يمكننا استخدام نظرية فيثاغورس لتحديد ما إذا كان المثلث قائم الزاوية أم لا.